Algoritmusok - Legrövidebb útvonalak

---

A Dijkstra-algoritmus egy hatékony módszer a legrövidebb útvonalak megtalálására egy súlyozott gráfban, ahol az élek nem negatív súlyúak. Edsger W. Dijkstra 1956-ban fejlesztette ki, és azóta széles körben alkalmazzák hálózati tervezésben, útvonaltervezésben és más optimalizálási feladatokban. Az algoritmus prioritási sort használ a csúcsok feldolgozásához, biztosítva, hogy a legrövidebb útvonalakat találja meg a kiindulási ponttól a célpontokig.

Gráf típusok

A Dijkstra algoritmus működését két fajta gráf típussal tudjuk modellezni és vizsgálni:

• Irányítatlan súlyozott (weighted undirected)
• Irányított súlyozott (weighted directed)

Mindkét gráf típus esetében a Dijkstra algoritmus hatékonyan találja meg a legrövidebb utat, feltéve, hogy nincsenek negatív élhosszak. Ha negatív élhosszak is előfordulnak, akkor a Dijkstra algoritmus nem biztosít helyes eredményt, és más algoritmusokra van szükség, például a Bellman-Ford algoritmusra.

Irányítatlan gráf

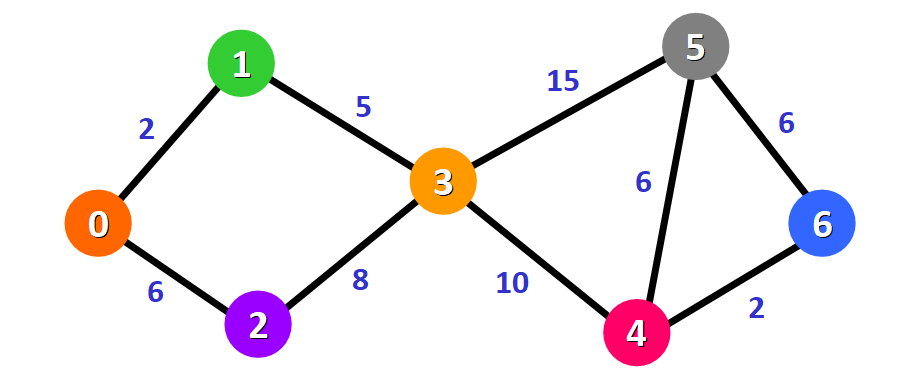
Ebben a típusban a gráf élei irányítatlanok, vagyis minden él kétirányú. Ha van egy él, amely összeköt két csúcsot, az mindkét irányban használható. A súlyok jellemzően azt mutatják meg, hogy milyen „költséggel” lehet átjutni egyik csúcsról a másikra.
A Dijkstra algoritmus működhet ilyen gráfok esetén is, az élek kétirányúsága miatt mindkét irányban figyelembe veszi a költséget.

Irányítatlan súlyozott gráf

Az fenti képen látható irányítatlan gráfban $7$ város található és mindegyik város között jelezve van, hogy mennyi az utazási idő (költség).

Célunk meghatározni a legrövidebb útvonalat a $0$ és $6$ városok között.

Lehetséges útvonalak

A $6$-os városba az alábbi városok érintésével juthatunk el:

Útvonal\(_n\)	Útvonal	Költség számítás	\(\sum_{költség}\)
1	$0 → 1 → 3 → 5 → 6$	2 + 5 + 15 + 6	28
2	$0 → 1 → 3 → 5 → 4 → 6$	2 + 5 + 15 + 6 + 2	30
3	$0 → 1 → 3 → 4 → 6$	2 + 5 + 10 + 2	19
4	$0 → 1 → 3 → 4 → 5 → 6$	2 + 5 + 10 + 6 + 6	29
5	$0 → 2 → 3 → 5 → 6$	6 + 8 + 15 + 6	35
6	$0 → 2 → 3 → 5 → 4 → 6$	6 + 8 + 15 + 6 + 2	37
7	$0 → 2 → 3 → 4 → 6$	6 + 8 + 10 + 2	26
8	$0 → 2 → 3 → 4 → 5 → 6$	6 + 8 + 10 + 6 + 6	36
			\(min_{költség}=\)19

Irányított gráf

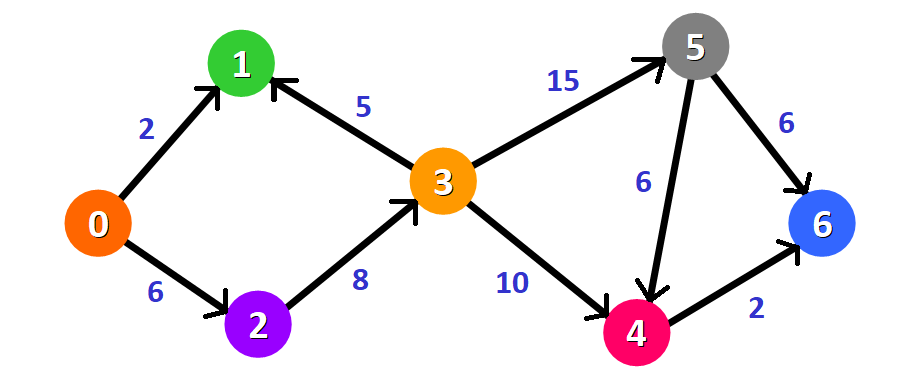
Ebben a gráfban az élek irányítottak, vagyis minden élnek van egy meghatározott iránya. Ha van egy él a -> b, akkor ez az él csak a-ból b-be használható, fordított irányban nem.
A Dijkstra algoritmus működik ilyen gráfokon is, figyelembe véve az élek irányát és súlyát. Csak olyan útvonalakat keres, amelyek az él irányával megegyezően haladnak.

Irányított súlyozott gráf

Az fenti képen látható irányított gráfban szintén $7$ város található és mindegyik város között jelezve van, hogy mennyi az utazási idő (költség).

Célunk meghatározni a legrövidebb útvonalat a $0$ és $6$ városok között.

Útvonal\(_n\)	Útvonal	Költség számítás	\(\sum_{költség}\)
1	$0 → 1 → 3 → 5 → 6$	2 + 5 + 15 + 6	28
2	$0 → 1 → 3 → 5 → 4 → 6$	2 + 5 + 15 + 6 + 2	30
3	$0 → 1 → 3 → 4 → 6$	2 + 5 + 10 + 2	19
4	$0 → 1 → 3 → 4 → 5 → 6$	2 + 5 + 10 + 6 + 6	29
5	$0 → 2 → 3 → 5 → 6$	6 + 8 + 15 + 6	35
6	$0 → 2 → 3 → 5 → 4 → 6$	6 + 8 + 15 + 6 + 2	37
7	$0 → 2 → 3 → 4 → 6$	6 + 8 + 10 + 2	26
8	$0 → 2 → 3 → 4 → 5 → 6$	6 + 8 + 10 + 6 + 6	36
			\(min_{költség}=\)19

Feladat

Adott $n$ darab város és $m$ darab repülési útvonal a városok között, de minden útvonal az első városból indul.
Cél, hogy meghatározzuk az első városból minden másik városba vezető legrövidebb út hosszát úgy, hogy figyelembe vesszük az átszállásos lehetőségeket is.

Input

Az input két részből áll: városok és járatok száma, illetve a repülési útvonalakat leíró sorok.

Az első bemeneti sorban két egész számot várunk: a városok és a járatok számát.
A városok számozottak: $1, 2, n$.

A repülési útvonalakat leíró sorok három egész számot tartalmaznak: indulási város, cél város és a két város között út hosszát. Minden járat egyirányú.

Output

Írassuk ki, hogy az első városból a többi városba mennyi a legrövidebb út hossza. A kimenet első értéke az önmagához vezető legrövidebb út legyen, ami ebben az esetben mindig 0 lesz.

Korlátozások

Futási limit: 1.00 s
Memória limit: 512 MB

$ 1 \le n \le 10^5 $
$1 \le m \le 2 \cdot 10^5$
$1 \le a,b \le n$
$1 \le c \le 10^9$

Példa

Input

3 4
1 2 6
1 3 2
3 2 3
1 3 4

Output

0 5 2

Unit Test

# Ha olyan megoldást használunk, amely a heapq könyvtárra épül:
# import heapq
import unittest

def dijkstra(n, graph):
    # Ide jön az algoritmus megoldása
    
# Tesztelhető segédfüggvény a bemenet feldolgozására
def parse_input(data):
    data = data.split()  # Input feldarabolása
    n = int(data[0])  # városok száma
    m = int(data[1])  # járatok száma

    graph = [[] for _ in range(n + 1)]

    index = 2
    for _ in range(m):
        a = int(data[index])
        b = int(data[index + 1])
        c = int(data[index + 2])
        index += 3
        graph[a].append((b, c))

    return n, graph

# Unittest osztály
class TestDijkstra(unittest.TestCase):
    
    # Példa input 1 tesztelése
    def test_case_1(self):
        input_data = "3 4\n1 2 6\n1 3 2\n3 2 3\n1 3 4"
        n, graph = parse_input(input_data)
        result = dijkstra(n, graph)
        expected_output = [0, 5, 2]  # Példa output 1
        self.assertEqual(result, expected_output)

    # Példa input 2 tesztelése
    def test_case_2(self):
        input_data = "3 4\n1 2 4\n1 3 2\n3 2 3\n1 3 4"
        n, graph = parse_input(input_data)
        result = dijkstra(n, graph)
        expected_output = [0, 4, 2]  # Példa output 2
        self.assertEqual(result, expected_output)

# main metódus, hogy futtassa az unittest-eket
if __name__ == "__main__":
    unittest.main()

Tesztelés (CSES)

A CSES oldalán bejelentkezést követően lehetőség van az algoritmusra írt megoldásunk futtatására és tesztelésére: https://cses.fi/problemset/submit/1671/

Lehetséges megoldások

Segédkönyvtárak (heapq) nélkül

def dijkstra(n, graph):
    # Távolságok kezdetben végtelenek
    distances = [float('inf')] * (n + 1)
    distances[1] = 0  # A kezdő város (1-es) távolsága 0
    visited = [False] * (n + 1)  # Jelzi, hogy meglátogattuk-e a várost

    while True:
        # Kiválasztjuk a legkisebb távolságú még nem látogatott várost
        min_distance = float('inf')
        u = -1
        for i in range(1, n + 1):
            if not visited[i] and distances[i] < min_distance:
                min_distance = distances[i]
                u = i

        # Ha nem találtunk ilyen várost, akkor kész vagyunk
        if u == -1:
            break

        # Megjelöljük, hogy ezt a várost most meglátogattuk
        visited[u] = True

        # Szomszédok feldolgozása
        for v, hossz in graph[u]:
            if distances[u] + hossz < distances[v]:
                distances[v] = distances[u] + hossz

    return distances[1:]

Ez a megoldás is jól működik bármilyen inputra alkalmazva, ugyanakkor nagyobb méretű inputok esetében nagyon lassú. A CSES-en futtatva a kódot ez bizonyosságot is nyer, hiszen 23 teszt esetből csak 6 esetben kapunk sikeres eredményt, 17 esetben pedig túl lépjük az időkorlátot, amely jelen esetben 1 másodperc.
A következő megoldással már nagyot javul a kódunk futási ideje, amelyet a heapq könyvtár használatával értünk el.

A heapq könyvtár használatával

import heapq

def dijkstra(n, graph):
    # Távolságok kezdetben végtelenek
    distances = [float('inf')] * (n + 1)
    distances[1] = 0  # A kezdő város (1-es) távolsága 0
    priority_queue = [(0, 1)]  # (távolság, város) -> 0 távolság a kezdő városra

    # Addig fut, amíg van elem a prioritási sorban
    while priority_queue:
        current_distance, u = heapq.heappop(priority_queue)

        # Ha a jelenlegi távolság nagyobb, mint a tárolt távolság, kihagyjuk
        if current_distance > distances[u]:
            continue

        # Szomszédok feldolgozása
        for v, hossz in graph[u]:
            distance = current_distance + hossz
            if distance < distances[v]:
                distances[v] = distance
                heapq.heappush(priority_queue, (distance, v))

    return distances[1:]

CSES teszt eredmények

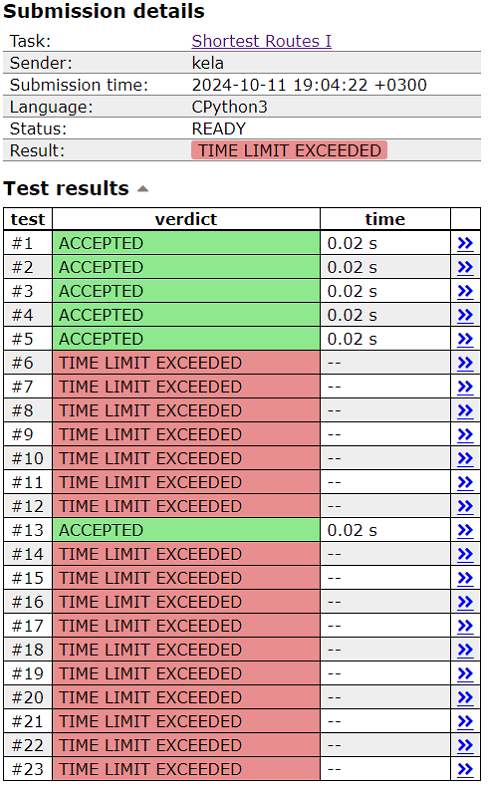heapq könyvtár használata nélkül elért futási eredmények 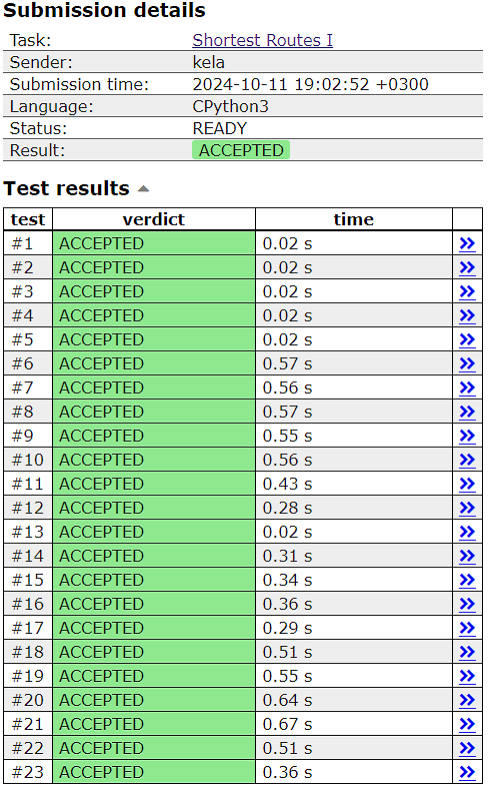heapq könyvtár használatával elért futási eredmények

Letölthető fájlok

•     UnitTest
•     CSES input (heapq)
•     CSES input (without heapq)
•     Megoldás + UnitTest (heapq)
•     Megoldás + UnitTest (without heapq)